

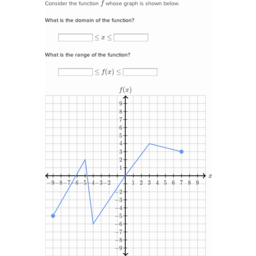
And that's a closed interval, where x could be 1, and We want to know the average rate of change of y with respect to x over the interval from And the first thing I'd like to tackle is think about the average rate of change of y with respect to x over the interval from xĮqualing 1 to x equaling 3. Is equal to x squared, or at least part of the graph So right over here we have the graph of y There are plenty of things in mathematics that have no real world application, though they are studied nonetheless. Lastly, "not having a purpose" (which is not the case with secant lines and average rates of change) is a poor argument for neglecting to study anything – especially in mathematics. Furthermore, if you are looking at discrete data (as is the case in every real world observation), there is no way to get an instantaneous rate of change from that data because it is not continuous.
In particular, in physics, there are a lot of phenomena that occur that have to deal with average rates of change instead of instantaneous rates of change.
Break even point formula graph khan academy how to#
As for "not bothering with the secant", there is no way to explain the process of finding instantaneous change without explaining how to find average change for the reason you just identified: the principles involved in finding average rate of change are part of finding instantaneous rate of change.Īlso, average rates of change have advantages in their own right. As you say, the process of finding the slope of the tangent line descends from the process of finding the slope of a secant line (the only difference is that a certain limit is taken of the difference quotient which is the expression for the slope of a general secant). For instance, you can calculate a monthly, weekly, or even daily break-even analysis to give your sales team a goal to aim for.ĭo you need help completing your break-even analysis? Connect with a SCORE mentor online or in your community today.Calculating average change using secant lines is actually an important intermediate step to finding instantaneous change via tangent lines (and thus also derivatives). For instance, if you add another employee to the payroll, how many extra sales dollars will be needed to recoup that additional expense? If you borrow money, how much will be needed to cover the monthly principal and interest payments?Ī break-even analysis can also be used as a motivational tool. In this situation, a break-even analysis can help you calculate how different scenarios might play out financially. Existing businesses can benefit from a break-even analysis, too. If your break-even analysis shows that it will take longer, you need to revisit your costs and pricing strategy so you can increase your margins and break even in a reasonable amount of time. In general, you should aim to break even in six to 18 months after launching your business. This will help you plan the amount of startup capital you’ll need and determine how long that capital will need to last. Financing sources will want to see when you expect to break even so they know when your business will become profitable.īut even if you’re not seeking outside financing, you should know when your business is going to break even.
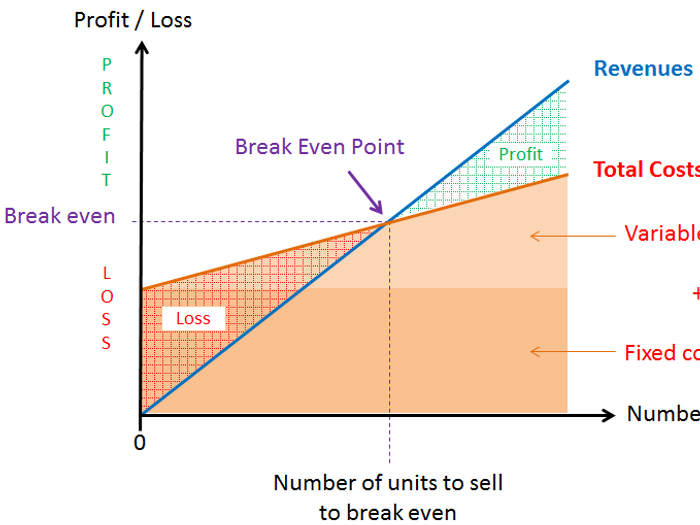
When Should You Use a Break-Even Analysis?Ī break-even analysis is a critical part of the financial projections in the business plan for a new business. To use this break-even analysis template, gather information about your business’s fixed and variable costs, as well as your 12-month sales forecast. Your business is “breaking even”-not making a profit but not losing money, either.Īfter the break-even point, any additional sales will generate profits. What is a break-even analysis? The break-even point is the point when your business’s total revenues equal its total expenses.


 0 kommentar(er)
0 kommentar(er)
